Everything is working on binary number system in computers, so it is valid in IP addresses as well.
Assume that IP address is 192.168.1.0 in dotted-decimal format is equal to 11000000.10101000.00000001.00000000 in dotted-binary format.
Assume that Subnet Mask is 255.255.255.0 in dotted-decimal format is equal to 11111111.11111111.11111111.00000000 in dotted-binary format. Subnet Mask is shown in /24 in slash notation(known as CIDR notation)
IP Address with Subnet Mask can be shown in CIDR notation 192.168.1.0/24
CIDR gives a concise way to represent both an IP network and its size using a combination of an IP address and a number after a slash.
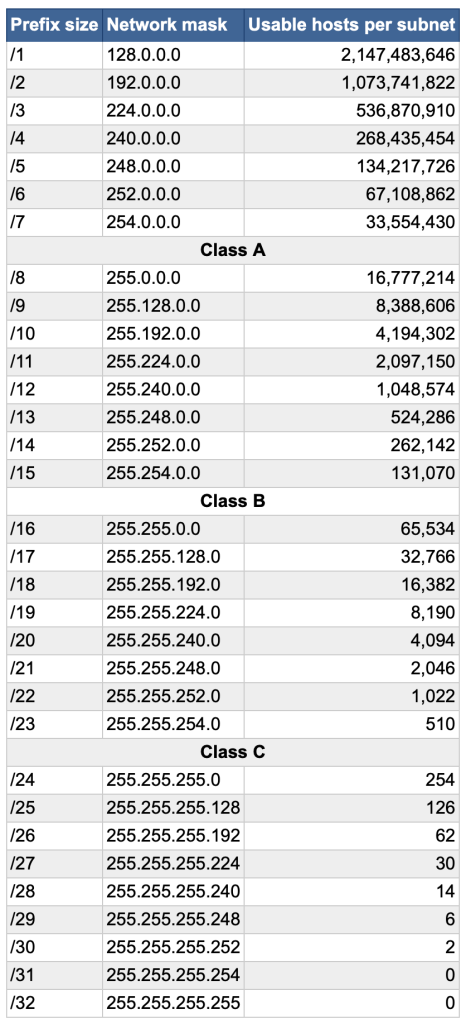
Subnet Mask is 24 after slash in decimal representation. In order to find out 24, Subnet mask should be represented in binary number system like 11111111.11111111.11111111.00000000. So, just count how many 1 bit there are in Subnet Mask.
IP Address and Subnet Mask in Decimal format:
IP Address: 192.168.1.0
Subnet Mask: 255.255.255.0
IP Address and Subnet Mask in CIDR format:
192.168.1.0/24
IP Address and Subnet Mask in Binary format:
IP Address: 11000000.10101000.00000001.00000000
Subnet Mask: 11111111.11111111.11111111.00000000
IPv4 Example
When referring to the blocks of an IPv4 address, like
192.168.1.0, it is appropriate to use the term "octet" to describe each block:
192is the first octet.168is the second octet.1is the third octet.0is the fourth octet.You can use this terminology regardless of whether the individual octets are being described in decimal, binary, octal, or any other number system.
The term "octet" refers to the underlying binary structure of each block in an IPv4 address. Each block, or octet, consists of 8 bits.
When you see an IP address written in the familiar decimal format, like
192.168.1.0, each of those decimal numbers corresponds to an 8-bit binary number:
192in decimal is11000000in binary.168in decimal is10101000in binary.1in decimal is00000001in binary.0in decimal is00000000in binary.So, even though we commonly represent and think about IP addresses in decimal format for simplicity and readability, the underlying representation in the computer is binary, with each octet consisting of 8 binary digits (bits).
CIDR stands for "Classless Inter-Domain Routing." It's a method for allocating IP addresses and routing IP packets. Before diving deeper into CIDR, let's understand some background.
Historically, IP addresses were allocated based on classes:
– Class A: Supported 16 million hosts on each of 128 networks.
– Class B: Supported 65,000 hosts on each of 16,000 networks.
– Class C: Supported 254 hosts on each of 2 million networks.
This system was inefficient and led to the waste of many IP addresses. As the internet grew, it became clear that this method of address allocation would not scale, leading to the development of CIDR to better utilize the IP address space.
IP Address with Subnet Mask
- CIDR's Introduction:
- The term "CIDR" represents a modern system used to manage and allocate IP addresses in networking.
- Combination of IP and Slash Notation:
- CIDR combines the traditional IP address and a slash notation to define a network and its size. This format is often referred to as "CIDR notation."
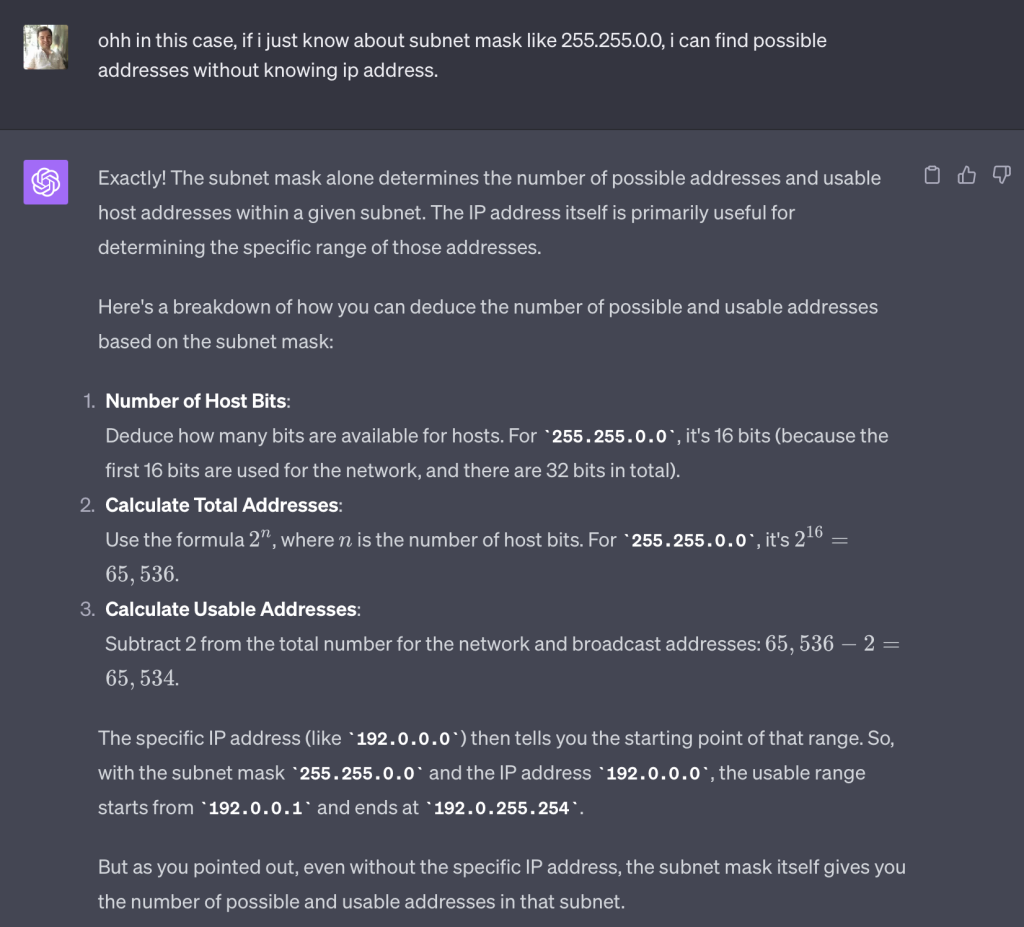
- Example – 192.168.1.0/24:
192.168.1.0is a typical IP address./24is the CIDR notation indicating the network's size or how many addresses it encompasses.- Together,
192.168.1.0/24tells us about a specific network and its size.- Range of IP Addresses:
- In the example
192.168.1.0/24, the range of IP addresses that belong to this network starts from192.168.1.0and ends at192.168.1.255.- Understanding the /24:
- The
/24in our example is a way to represent the subnet mask.- It says that the first 24 bits of the IP address specify the network, and the remaining bits (32 total bits in an IPv4 address – 24 network bits = 8 bits) specify individual devices or hosts in that network.
- In binary form, 24 consecutive '1' bits look like:
11111111.11111111.11111111.00000000- This binary form translates to the decimal subnet mask
255.255.255.0.In simple terms, CIDR gives a concise way to represent both an IP network and its size using a combination of an IP address and a number after a slash. This method makes it easier to understand and manage networks.
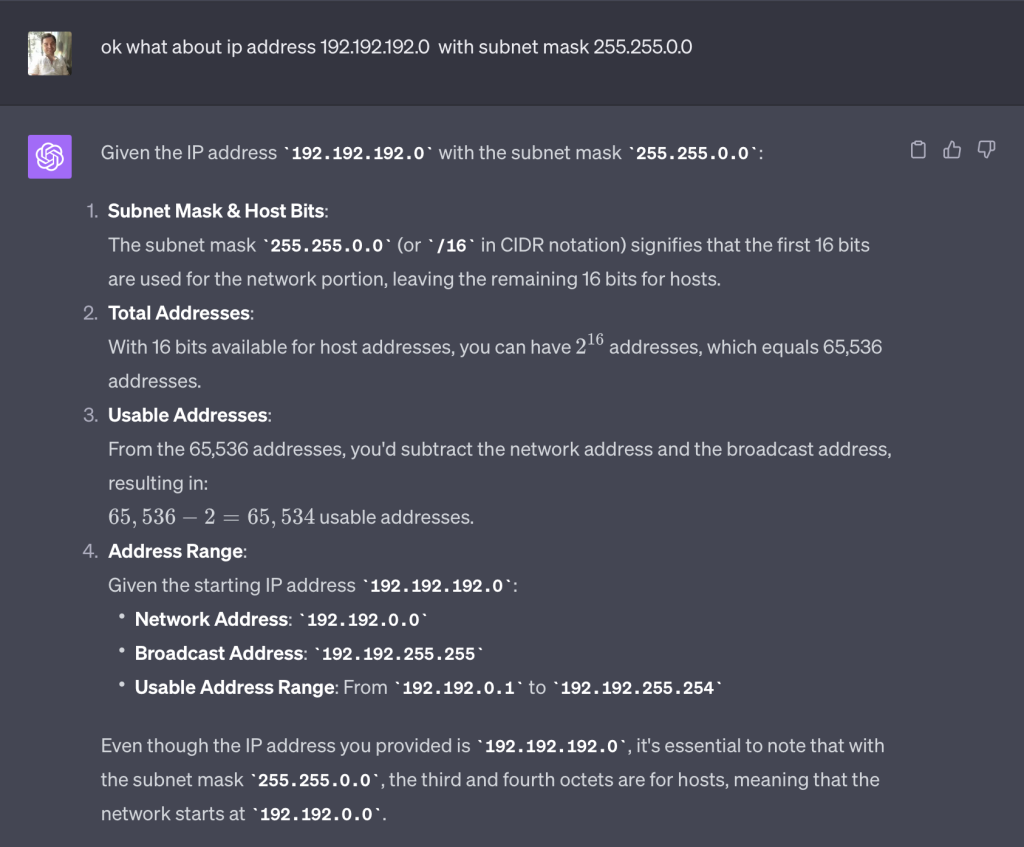
The string you provided is an IP address in binary notation. It represents the subnet mask for a
/24network in CIDR notation.Let's break down this binary representation:
11111111in binary is equivalent to255in decimal.00000000in binary is equivalent to0in decimal.So, when we convert each of the binary octets in
11111111.11111111.11111111.00000000to decimal, we get:
255.255.255.0This is a common subnet mask. In CIDR notation, it's often represented as
/24, as mentioned in the previous explanations. This means the first 24 bits (three octets) are used for the network portion, and the remaining 8 bits (one octet) are used for host addresses within that network.
Understanding Subnet Mask
The binary representation11111111.11111111.11111110.00000000is indeed a valid subnet mask.Let's convert each octet to its decimal equivalent:
11111111in binary is equivalent to255in decimal.11111111in binary is equivalent to255in decimal.11111110in binary is equivalent to254in decimal.00000000in binary is equivalent to0in decimal.So, the subnet mask in decimal notation is:
255.255.254.0In CIDR notation, this would be represented as
/23because there are 23 consecutive '1' bits in the subnet mask.This means that the first 23 bits are used for the network portion, and the remaining 9 bits are for the host addresses within that network.

Number System
There's an infinite number of possible number systems, because a number system is defined by its base, and there's no limit to the number of possible bases. However, in practice and especially in mathematics and computing, we commonly refer to a few specific bases. Here are some of them:
- Binary (Base-2): Uses two digits (0 and 1). It's fundamental to computer systems and digital logic.
- Ternary (Base-3): Uses three digits (0, 1, and 2). It's less common, but has been explored for certain computational structures.
- Quaternary (Base-4): Uses four digits (0, 1, 2, and 3).
- Quinary (Base-5): Uses five digits (0 through 4).
- Decimal (Base-10): The standard system for everyday math and most human activities. It uses ten digits (0 through 9).
- Octal (Base-8): Uses eight digits (0 through 7). It was more commonly used in earlier computing systems.
- Duodecimal (Base-12): Uses twelve distinct symbols. Some people have advocated for its use in everyday life due to the divisibility properties of 12.
- Hexadecimal (Base-16): Uses sixteen distinct symbols (0-9 and then A-F). It's widely used in computing.
- Vigesimal (Base-20): Uses twenty distinct symbols. Some ancient civilizations, like the Mayans, used this system.
- Sexagesimal (Base-60): Uses sixty distinct symbols. The ancient Babylonians used this system, and its remnants are still seen today in our time measurements (60 seconds in a minute, 60 minutes in an hour) and angular measurements (360 degrees in a circle).
Other bases exist and can be constructed or thought of, but the ones listed above are among the most noteworthy either due to their historical significance, their application in certain areas, or their mathematical properties.
In modern mathematics and other disciplines, it's possible to work in arbitrary bases. For instance, "base-n" refers to a numeral system that uses n symbols. However, for many purposes, the above systems (especially binary, decimal, and hexadecimal) are the most relevant.
- Binary (Base-2):
- Uses only two digits: 0 and 1.
- Every position in a binary number represents a power of 2, with the rightmost position being 2020 (or 1).
- Example: The binary number
1011represents 1(23)+0(22)+1(21)+1(20)=8+0+2+1=111(23)+0(22)+1(21)+1(20)=8+0+2+1=11 in decimal.- Octal (Base-8):
- Uses eight digits: 0 through 7.
- Every position in an octal number represents a power of 8.
- Example: The octal number
547represents 5(82)+4(81)+7(80)=320+32+7=3595(82)+4(81)+7(80)=320+32+7=359 in decimal.- Hexadecimal (Base-16):
- Uses sixteen distinct digits. The first ten are the same as the decimal system (0 through 9), and the next six are represented as 'A' (for ten) through 'F' (for fifteen).
- Every position in a hexadecimal number represents a power of 16.
- Example: The hexadecimal number
2A3represents 2(162)+10(161)+3(160)=512+160+3=6752(162)+10(161)+3(160)=512+160+3=675 in decimal. (Note that A represents 10 in decimal.)Why do we use them?
- Binary is fundamental because computers operate on binary logic. All operations in a computer's hardware are, at their core, binary operations.
- Octal was more popular in the past, especially with some old computer systems. It's less common now but can sometimes be seen in specific applications like UNIX file permissions.
- Hexadecimal is very useful in computing because it represents a byte (8 bits) with just two characters (since 162=256162=256). It's often used in programming, memory addressing, and defining colors in web design (e.g., RGB values).
There are primarily two versions of IP addresses: IPv4 and IPv6. Each of these versions has its own format and representation:
- IPv4 (Internet Protocol version 4):
- Uses a 32-bit address scheme.
- Displayed as four decimal numbers separated by periods (dots).
- Each of the four numbers can range from 0 to 255.
- Example:
192.168.1.1.- IPv6 (Internet Protocol version 6):
- Uses a 128-bit address scheme.
- Displayed as eight groups of four hexadecimal digits separated by colons.
- Leading zeros in each group can be omitted, and consecutive groups of zeros can be represented as a double colon (
::).- Example:
1200:0000:AB00:1234:0000:2552:7777:1313can be shortened to1200:0:AB00:1234:0:2552:7777:1313or even further to1200::AB00:1234:0:2552:7777:1313.